某仓库在某天运进和运出一批货物，运进为“+”，运出为“-”，单位为“吨”．记录如下：+30，-15，+25，-10，-18，+40，-17，-23．

（1）若原库存为10吨，则当天最终库存多少吨？

（2）若运进运出每车费用50元，一车装5吨，则当天总运费为多少元？

邮政部门规定：信函重100克以内（包括100克）每20克贴邮票0.8元，不足20克重以20克计算；超过100克，先贴邮票4元，超过100克部分每100克加贴邮票2元，不足100克重以100克计算．
（1）若要寄一封重35克的信函，则需贴邮票多少元？
（2）若寄一封信函贴了6元邮票，问此信函可能有多少重？
（3）七（1）班有九位同学参加环保知识竞赛，若每份答卷重12克，每个信封重4克．请你设计方案，将这9份答卷分装在两个信封中寄出，使所贴邮票的总金额最少．

足球射门，不考虑其他因素，仅考虑射点到球门AB的张角大小时，张角越大，射门越好．如图的正方形网格中，点A，B，C，D，E均在格点上，球员带球沿CD方向进攻，最好的射点在（　　）

A．点C                                     B．点D或点E

C．线段DE（异于端点） 上一点                 D．线段CD（异于端点） 上一点

小明的爸爸和妈妈分别驾车从家同时出发去上班，爸爸行驶到甲处时，看到前面路口时红灯，他立即刹车减速并在乙处停车等待，爸爸驾车从家到乙处的过程中，速度v（m/s）与时间t（s）的关系如图1中的实线所示，行驶路程s（m）与时间t（s）的关系如图2所示，在加速过程中，s与t满足表达式s=at²

（1）根据图中的信息，写出小明家到乙处的路程，并求a的值；

（2）求图2中A点的纵坐标h，并说明它的实际意义；

（3）爸爸在乙处等待7秒后绿灯亮起继续前行，为了节约能源，减少刹车，妈妈驾车从家出发的行驶过程中，速度v（m/s）与时间t（s）的关系如图1中的折线O﹣B﹣C所示，行驶路程s（m）与时间t（s）的关系也满足s=at²，当她行驶到甲处时，前方的绿灯刚好亮起，求此时妈妈驾车的行驶速度．

如图，在直角坐标系中，点A，B分别在x轴，y轴上，点A的坐标为（﹣1，0），∠ABO=30°，线段PQ的端点P从点O出发，沿△OBA的边按O→B→A→O运动一周，同时另一端点Q随之在x轴的非负半轴上运动，如果PQ=，那么当点P运动一周时，点Q运动的总路程为　 　．

把数字1，2，3，4，5，6，7，8，9分别填入下图的9个圈内，要求三角形ABC和三角形DEF的每条边上三个圈内数字之和等于18.

（1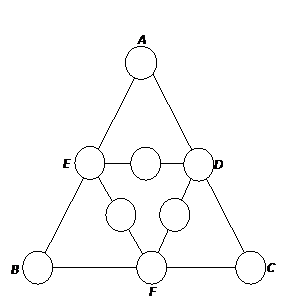）       给出一个符合要求的填法（直接填入圈中）；

（2）       共有多少种不同填法？证明你的结论.

13个小朋友围成一圈做游戏，规则是从某一个小朋友开始按顺时针方向数数，数到第13，该小朋友离开；这样继续下去，直到最后剩下一个小朋友．小明是1号，要使最后剩下的是小明自己，他应该建议从（　　）小朋友开始数起．

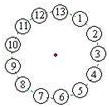
(A) 7号

（B）8号

（C）13号

（D）2号

选择题：

如图，甲、乙两动点分别从正方形ABCD的顶点A、C同时沿正方形的边开始运动，甲点依顺时针方向环行，乙点依逆时针方向环行，若乙的速度是甲的4倍，则它们第2015次相遇在边（  ）

(A) AB上     (B)BC上    (C)CD上    (D)DA上

   A   甲      D

                                     乙 

   B           C

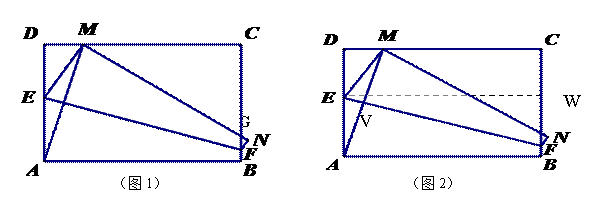
若在矩形ABCD中，AB=6，AD=4，将矩形进行折叠，使顶点A与CD边上的点M重合，折痕交AD于E，交BC于F，边AB折叠后BC与交于点G.

⑴若DM=1时，求DE和CG的长；

(2)设DM的长为x，梯形CDEF的面积为S，那么是否存在S的最大值？若存在，请求出这个最大值及此时x的值；若不存在，请说明理由.

（2015年金华）图1，图2为同一长方体房间的示意图，图2为该长方体的表面展开图.

（1）蜘蛛在顶点处

     ①苍蝇在顶点B处时，试在图1中画出蜘蛛为捉住苍蝇，沿墙面爬行的最近路线；

     ②苍蝇在顶点C处时，图2中画出了蜘蛛捉住苍蝇的两条路线，往天花板ABCD爬行的最近路线和往墙面爬行的最近路线，试通过计算判断哪条路线更近？ 
（2）在图3中，半径为10dm的⊙M与相切，圆心M到边的距离为15dm，蜘蛛P在线段AB上，苍蝇Q在⊙M的圆周上，线段PQ为蜘蛛爬行路线。若PQ与⊙M相切，试求PQ的长度的范围.