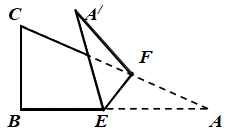
如图，中，E，F分别是边AB，AC上的点，连结EF，将沿着EF折叠，得到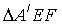，当的三边与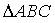的三边有一组边平行时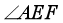，的度数不可能是 （   ）

A. 120⁰    B. 105⁰     C. 75⁰      D. 45⁰

如图，矩形ABCD 中，AB＝4，AD＝3，M 是边CD 上一点，将△ADM沿直线AM对折，得到△ANM．

（1）当AN平分∠MAB时，求DM的长；

（2）连接BN ，当DM＝1时，求△ABN的面积；

（3）当射线BN 交线段CD于点F时，求DF的最大值．

如图，矩形ABCD中，BC=2，将矩形ABCD绕点D顺时针旋转90°，点A、C分别落在点A′、C′ 处．如果点A′、C′、B在同一条直线上，那么tan∠ABA′ 的值为        

如图1，在直角坐标系xoy中，直线l：y=kx+b交x轴，y轴于点E，F，点B的坐标是（2，2），过点B分别作x轴、y轴的垂线，垂足为A、C，点D是线段CO上的动点，以BD为对称轴，作与△BCD或轴对称的△BC′D．

（1）当∠CBD=15°时，求点C′的坐标．

（2）当图1中的直线l经过点A，且k=﹣时（如图2），求点D由C到O的运动过程中，线段BC′扫过的图形与△OAF重叠部分的面积．

（3）当图1中的直线l经过点D，C′时（如图3），以DE为对称轴，作于△DOE或轴对称的△DO′E，连结O′C，O′O，问是否存在点D，使得△DO′E与△CO′O相似？若存在，求出k、b的值；若不存在，请说明理由．

在平面直角坐标系中，点O为原点，点A的坐标为（﹣6，0）．如图1，正方形OBCD的顶点B在x轴的负半轴上，点C在第二象限．现将正方形OBCD绕点O顺时针旋转角α得到正方形OEFG． （1）如图2，若α=60°，OE=OA，求直线EF的函数表达式． （2）若α为锐角，tanα= ，当AE取得最小值时，求正方形OEFG的面积． （3）当正方形OEFG的顶点F落在y轴上时，直线AE与直线FG相交于点P，△OEP的其中两边之比能否为 ：1？若能，求点P的坐标；若不能，试说明理由.

如图，在矩形ABCO中，点O为坐标原点，点B的坐标为(4，3)，点A，C在坐标轴上，点P在BC边上，直线:y=2x＋3，直线：y =2 x－3

  (1)分别求直线与x轴、直线与AB的交点坐标．

  (2)已知点M在第一象限，且是直线上的点，若∆APM是等腰直角三角形，求点M的坐标．

(3)我们把直线和直线上的点所组成的图形称为图形F．已知矩形ANPQ的顶点N在图形F上，Q是坐标平面内的点，且N点的横坐标 为x，请直接写出x的取值范围.

如图，矩形ABCD中，AB＝4，BC＝2，E是AB的中点，直线l平行于直线EC，且直线l与直线EC之间的距离为2，点F在矩形ABCD边上，将矩形ABCD沿直线EF折叠，使点A恰好落在直线l上，则DF的长为 __________ ．

我们定义：有一组邻角相等的凸四边形叫做“等邻角四边形”

（1）概念理解：

请你根据上述定义举一个等邻角四边形的例子；

（2）问题探究；

如图1，在等邻角四边形ABCD中，∠DAB=∠ABC，AD，BC的中垂线恰好交于AB边上一点P，连结AC，BD，试探究AC与BD的数量关系，并说明理由；

（3）应用拓展；

如图2，在Rt△ABC与Rt△ABD中，∠C=∠D=90°，BC=BD=3，AB=5，将Rt△ABD绕着点A顺时针旋转角α（0°＜∠α＜∠BAC）得到Rt△AB′D′（如图3），当凸四边形AD′BC为等邻角四边形时，求出它的面积．

七巧板是我们祖先的一项卓越创造，被誉为“东方魔板”，小明利用七巧板（如图1所示）中各板块的边长之间的关系拼成一个凸六边形（如图2所示），则该凸六边形的周长是            cm．

如图，点D在△ABC的边BC上，且与B，C不重合，过点D作AC的平行线DE交AB于E，作AB的平行线DF交AC于点F. 又知BC=5.

（1）设△ABC的面积为S. 若四边形AEDF的面积为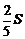，求BD的长.

（2）若AC=AB，且DF经过△ABC的重心G，求E，F两点间的距离.