-
-
如图,
 中,
中,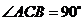 ,
,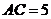 ,
, ,
,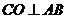 于点
于点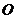 ,
, 是线段
是线段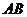 上一点,
上一点,
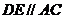 ,(
,(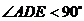 ),连接
),连接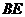 、
、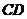 ,设
,设 中点分别为
中点分别为 .
.(1)求
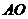 的长;
的长;(2)求
 的长;
的长;(3)若
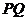 与
与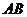 交于点
交于点 ,请直接写出
,请直接写出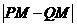 的值.
的值.
-
-
-
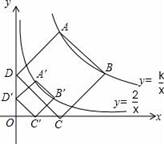
如图,正方形ABCD的顶点A,B在函数y=
 (x>0)的图象上,点C,D分别在x轴,y轴的正半轴上,当k的值改变时,正方形ABCD的大小也随之改变.
(x>0)的图象上,点C,D分别在x轴,y轴的正半轴上,当k的值改变时,正方形ABCD的大小也随之改变.(1)当k=2时,正方形A′B′C′D′的边长等于 .
(2)当变化的正方形ABCD与(1)中的正方形A′B′C′D′有重叠部分时,k的取值范围是 .
-
-
-
由6根钢管首尾顺次铰接而成六边形钢架ABCDEF,相邻两钢管可以转动.已知各钢管的长度为AB=DE=1米,BC=CD=EF=FA=2米.(铰接点长度忽略不计)
(1)转动钢管得到三角形钢架,如图1,则点A,E之间的距离是 米.
(2)转动钢管得到如图2所示的六边形钢架,有∠A=∠B=∠C=∠D=120°,现用三根钢条连接顶点使该钢架不能活动,则所用三根钢条总长度的最小值是 米.

图1 图2
-
-
-
在矩形纸片
 的正中间,摆放一个菱形
的正中间,摆放一个菱形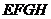 ,形成如图所示的轴对称图形.已知
,形成如图所示的轴对称图形.已知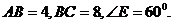 现将矩形纸片折叠,使矩形的顶点C与对角线交点O重合,折痕为MN,如图2所示.如果菱形的顶点G恰好落在折痕MN上,则菱形EFGH的面积为 .
现将矩形纸片折叠,使矩形的顶点C与对角线交点O重合,折痕为MN,如图2所示.如果菱形的顶点G恰好落在折痕MN上,则菱形EFGH的面积为 .

-
-
-
直线
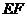 上有两点
上有两点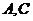 ,分别引两条射线
,分别引两条射线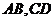 .
.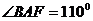 ,
,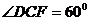 ,射线
,射线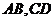 分别绕
分别绕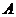 点,
点,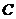 点以1度/秒和3度/秒的速度同时顺时针转动,设时间为
点以1度/秒和3度/秒的速度同时顺时针转动,设时间为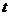 ,在射线
,在射线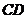 转动一周的时间内,则
转动一周的时间内,则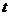 = 秒,
= 秒,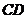 与
与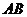 平行.
平行.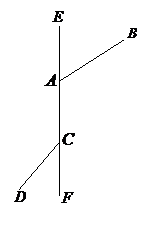
-
-
-
已知点
 与点
与点 是一个平行四边形的四个顶点,则
是一个平行四边形的四个顶点,则 长的最小值为( )
长的最小值为( ) A. 4 B.
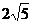 C.
C.  D.
D. 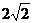
-
-
-
如图,
 的面积为1,
的面积为1,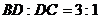 ,
,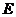 是
是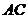 的中点,
的中点,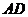 与
与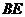 相交于点
相交于点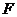 ,那么四边形
,那么四边形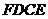 的面积为 .
的面积为 .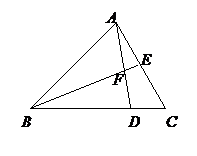
-
-
-
在
 中,AD是BC边上的高线,CE 是AB边上的中线,
中,AD是BC边上的高线,CE 是AB边上的中线, ⊥CE 于G,CD =AE.
⊥CE 于G,CD =AE.(1) 求证:CG =EG;
(2)
 若AD =6,BD =8,求CE 的长.
若AD =6,BD =8,求CE 的长.
-
-
-
已知在△ABC中,AD是BC边上的高线,CE是AB边上的中线,DG⊥CE于G,CD=AE.(1)写出CG与EG的数量关系,并说明理由.(2)若AD=12,AB=20,求CE的长.
-
-
-
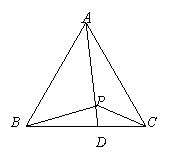 在等边
在等边 中,D是BC边上的一点,且BD=2CD,P是AD上的一点,
中,D是BC边上的一点,且BD=2CD,P是AD上的一点, 求证:
求证:
-
浙江安吉导学网络科技有限公司 版权所有 浙ICP备2021004467号-1 浙公网安备33052302000911号
浙公网安备33052302000911号
※有关作品版权事宜请联系:13083908525 邮箱:zcb7525@163.com