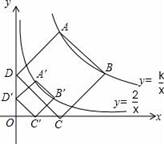
如图,正方形ABCD的顶点A,B在函数y= (x>0)的图象上,点C,D分别在x轴,y轴的正半轴上,当k的值改变时,正方形ABCD的大小也随之改变.
(x>0)的图象上,点C,D分别在x轴,y轴的正半轴上,当k的值改变时,正方形ABCD的大小也随之改变.
(1)当k=2时,正方形A′B′C′D′的边长等于 .
(2)当变化的正方形ABCD与(1)中的正方形A′B′C′D′有重叠部分时,k的取值范围是 .
答案
解(1):当k=2时,如图,分别过点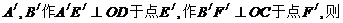
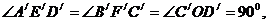
 正方形A′B′C′D′,
正方形A′B′C′D′,
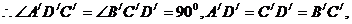
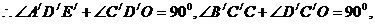
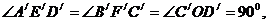
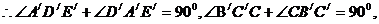
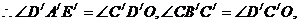
又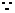
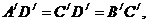
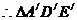 ≌
≌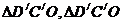 ≌
≌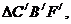
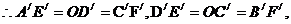
设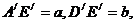 则
则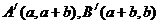
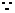 点
点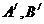 在函数
在函数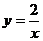 (x>0)的图象上,
(x>0)的图象上,
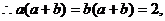 解得
解得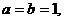

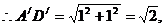 即当k=2时,正方形A′B′C′D′的边长等于
即当k=2时,正方形A′B′C′D′的边长等于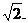
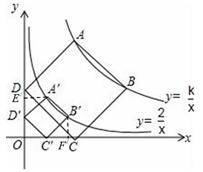
解(2):如图,分别延长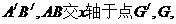 分别过点
分别过点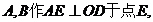
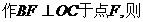 由上述(1)解答过程可得
由上述(1)解答过程可得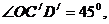
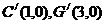
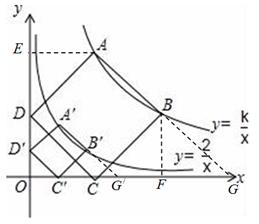
设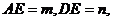 则与上述(1)解答过程同样,可得
则与上述(1)解答过程同样,可得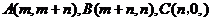
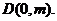
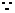 点A,B在函数
点A,B在函数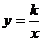 (x>0)的图象上,
(x>0)的图象上,
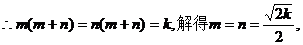
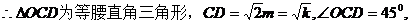
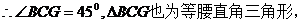
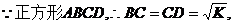
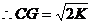
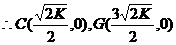
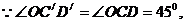
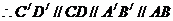
 当变化的正方形ABCD与(1)中的正方形A′B′C′D′有重叠部分时,
当变化的正方形ABCD与(1)中的正方形A′B′C′D′有重叠部分时,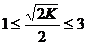 或
或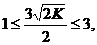
解得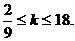
即当变化的正方形ABCD与(1)中的正方形A′B′C′D′有重叠部分时,k的取值范围是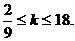
解析
正确解答该题的关键在于,数形结合,分类讨论周全.
 浙公网安备33052302000911号
浙公网安备33052302000911号