-
-
已知抛物线C:y=x2﹣2x+1的顶点为P,与y轴的交点为Q,点F(1,
 ).
).(Ⅰ)求点P,Q的坐标;
(Ⅱ)将抛物线C向上平移得到抛物线C′,点Q平移后的对应点为Q′,且FQ′=OQ′.
①求抛物线C′的解析式;
②若点P关于直线Q′F的对称点为K,射线FK与抛物线C′相交于点A,求点A的坐标.
-
-
-
如图,抛物线y=x2﹣mx﹣3(m>0)交y轴于点C,CA⊥y轴,交抛物线于点A,点B在抛物线上,且在第一象限内,BE⊥y轴,交y轴于点E,交AO的延长线于点D,BE=2AC.
(1)用含m的代数式表示BE的长.
(2)当m=
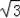 时,判断点D是否落在抛物线上,并说明理由.
时,判断点D是否落在抛物线上,并说明理由.(3)若AG∥y轴,交OB于点F,交BD于点G.
①若△DOE与△BGF的面积相等,求m的值.
②连结AE,交OB于点M,若△AMF与△BGF的面积相等,则m的值是 .

-
-
-
已知点P在一次函数y=kx+b(k,b为常数,且k<0,b>0)的图象上,将点P向左平
移1个单位,再向上平移2个单位得到点Q,点Q也在该函数y=kx+b的图象上.
(1)k的值是 ;
(2)如图,该一次函数的图象分别与x轴、y轴交于A,B两点,且与反比例函数
 图象交于C,D两点(点C在第二象限内),过点C作CE⊥x轴于点E,记S1为四边形CEOB的面积,S2为△OAB的面积,若
图象交于C,D两点(点C在第二象限内),过点C作CE⊥x轴于点E,记S1为四边形CEOB的面积,S2为△OAB的面积,若 则b的值是 .
则b的值是 .
-
-
-
如图,平面直角坐标系中,平行四边形
 的顶点
的顶点 ,边
,边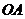 落在
落在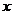 正半轴上,
正半轴上, 为线段
为线段 上一点,过点
上一点,过点 分别作
分别作 //
//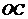 ,
, //
// 交平行四边形各边如图,若反比例函数
交平行四边形各边如图,若反比例函数 的图象经过点
的图象经过点 ,四边形
,四边形 的面积为6,则
的面积为6,则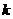 的值为( )
的值为( )A.18 B. 16 C. 12 D. 10

-
-
-
如图,在平面直角坐标系中,点A(10,0),以OA为直径在第一象限内作半圆,B为半圆上一点,连接AB并延长至C,使BC=AB,过C作 轴轴于点D,交线段OB于点E,已知CD=8,抛物线经过O、E、A三点,若P为抛物线上位于第一象限内的一个动点.以P、O、A、E为顶点的四边形面积记作S,当相应的点P有且只有3个时,则S的值是 .
轴轴于点D,交线段OB于点E,已知CD=8,抛物线经过O、E、A三点,若P为抛物线上位于第一象限内的一个动点.以P、O、A、E为顶点的四边形面积记作S,当相应的点P有且只有3个时,则S的值是 .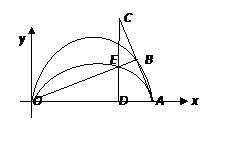
-
-
-
已知二次函数
 (
( ),当
),当 时,都有
时,都有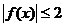 成立,且
成立,且 ,则
,则 .
.
-
-
-
在平面直角坐标系中,直线
 分别交
分别交 轴,
轴, 轴于A,B,直线
轴于A,B,直线 分别交
分别交 轴,
轴, 轴于C,D,直线AB, CD相交于E.
轴于C,D,直线AB, CD相交于E.(1)求点E的坐标;
(2)点P为线段AE上的一点,过点P作x轴的平行线分别交直线CB, CD于F, G,若P点的横坐标为m,设d=PF+PG,求d与m的函数关系式(直接写出自变量m的取值范围);
(3)在(2)的条件下,当直线EF把
 BCD的面积分成1:2两部分时,求m的值.
BCD的面积分成1:2两部分时,求m的值.

-
浙江安吉导学网络科技有限公司 版权所有 浙ICP备2021004467号-1 浙公网安备33052302000911号
浙公网安备33052302000911号
※有关作品版权事宜请联系:13083908525 邮箱:zcb7525@163.com