如图,在平面直角坐标系中,点A(10,0),以OA为直径在第一象限内作半圆,B为半圆上一点,连接AB并延长至C,使BC=AB,过C作 轴轴于点D,交线段OB于点E,已知CD=8,抛物线经过O、E、A三点,若P为抛物线上位于第一象限内的一个动点.以P、O、A、E为顶点的四边形面积记作S,当相应的点P有且只有3个时,则S的值是 .
轴轴于点D,交线段OB于点E,已知CD=8,抛物线经过O、E、A三点,若P为抛物线上位于第一象限内的一个动点.以P、O、A、E为顶点的四边形面积记作S,当相应的点P有且只有3个时,则S的值是 .
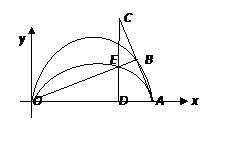
答案
解:如图1,连结OC,作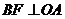 于点F.
于点F.
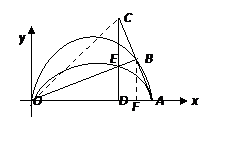
图1
 OA为直径,B为半圆上一点,
OA为直径,B为半圆上一点,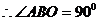
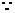 BC=AB
BC=AB
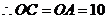
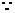
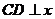 轴轴于点D
轴轴于点D
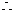
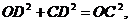
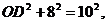 解得
解得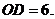
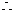
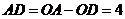
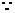
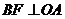 于点F
于点F
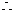
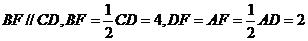
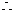
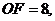 点
点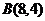
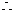 直线
直线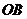 的解析式为
的解析式为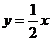 ,当
,当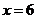 时,
时,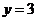 ,
,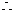
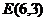
设抛物线解析式为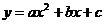 ,则
,则
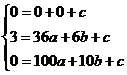 ,解得
,解得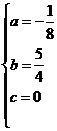 ,
,
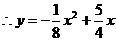
设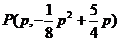 ,则
,则
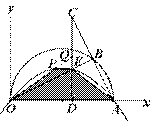
图2
(1)若点P在CD的左侧,延长OP交CD于Q,如图2,
OP所在直线解析式为: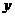 =
=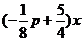
∴当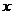 =6时,
=6时,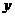 =
=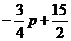 ,即Q点纵坐标为
,即Q点纵坐标为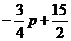 ,
,
∴QE=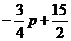 -3=
-3=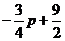 ,
,
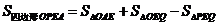
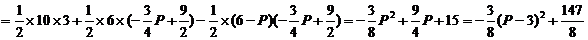 (2)若点P在CD的右侧,延长AP交CD于Q,如图3,
(2)若点P在CD的右侧,延长AP交CD于Q,如图3,

图3
设直线AP的解析式为:y=kx+d,把P和A坐标代入得,
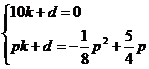 ,解得
,解得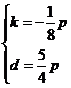 ,
,
∴直线AP的解析式为:
∴当x=6时,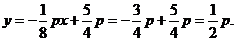 即Q点纵坐标为
即Q点纵坐标为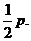 ,
,
∴QE=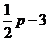
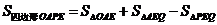
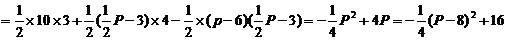
∴当P在CD右侧时,四边形OAPE的面积最大值为16,此时点P的位置只有一个,
又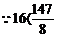 ∴当P在CD左侧时,四边形OPEA的面积等于16的对应P的位置有两个,
∴当P在CD左侧时,四边形OPEA的面积等于16的对应P的位置有两个,
当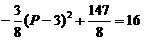 时,
时,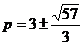
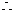 当相应的点P有且只有3个时,则S的值是16.
当相应的点P有且只有3个时,则S的值是16.
解析
正确解得该题的关键在于,分别求出点P在CD左侧、右侧时S的表达式.
 浙公网安备33052302000911号
浙公网安备33052302000911号