在平面直角坐标系中,直线 分别交
分别交 轴,
轴, 轴于A,B,直线
轴于A,B,直线 分别交
分别交 轴,
轴, 轴于C,D,直线AB, CD相交于E.
轴于C,D,直线AB, CD相交于E.
(1)求点E的坐标;
(2)点P为线段AE上的一点,过点P作x轴的平行线分别交直线CB, CD于F, G,若P点的横坐标为m,设d=PF+PG,求d与m的函数关系式(直接写出自变量m的取值范围);
(3)在(2)的条件下,当直线EF把 BCD的面积分成1:2两部分时,求m的值.
BCD的面积分成1:2两部分时,求m的值.
 | |||
 | |||
答案
解(1) 由已知得
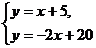 解得
解得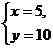
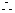 E(5,10)
E(5,10)
(2)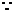 直线AB:
直线AB: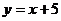 ,
,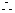 P(m,m+5)
P(m,m+5)
当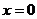 时,
时,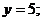 当
当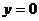 时,
时,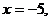
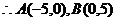
同理,由直线CD: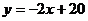 可得C(10,0),D(0,20)
可得C(10,0),D(0,20)
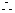 直线CB解析式为
直线CB解析式为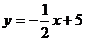 ,
,
由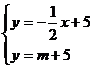 得:
得: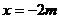 ,
,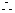 F(-2m,m+5)
F(-2m,m+5)
由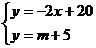 得:
得: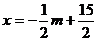 ,
, G(
G(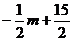 ,m+5)
,m+5)
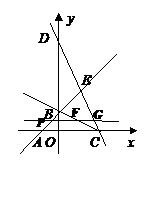 若点P在线段AB上,则
若点P在线段AB上,则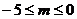 ,如图
,如图
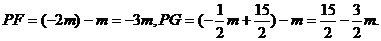
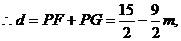 其中
其中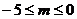 .
.
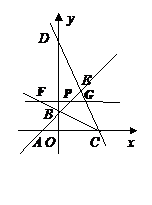 若点P在线段BE上,则
若点P在线段BE上,则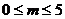 ,如图
,如图
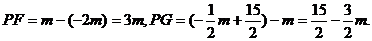
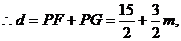 其中
其中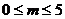 .
.
(3)由(1)、(2)已得:E(5,10),C(10,0),D(0,20), 点E为线段CD的中点.
点E为线段CD的中点.
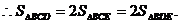
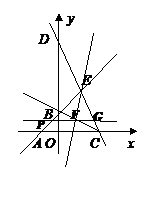 ①当
①当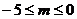 时,如图,
时,如图,
当直线EF把 BCD的面积分成1:2两部分时,
BCD的面积分成1:2两部分时,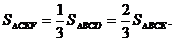
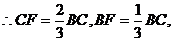
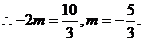
②当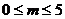 时,记直线EF交y轴于点R,如图,
时,记直线EF交y轴于点R,如图,
 |
当直线EF把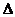 BCD的面积分成1:2两部分时,
BCD的面积分成1:2两部分时,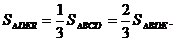
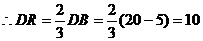 ,OR=10,
,OR=10, R(0,10)
R(0,10)
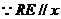 轴,
轴,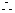 m+5=10,m=5.
m+5=10,m=5.
 当直线EF把
当直线EF把 BCD的面积分成1:2两部分时,m=
BCD的面积分成1:2两部分时,m=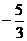 或5.
或5.
解析
解这题的关键在于,充分利用已知条件,分类讨论.
 浙公网安备33052302000911号
浙公网安备33052302000911号