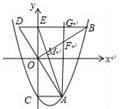
如图,抛物线y=x2﹣mx﹣3(m>0)交y轴于点C,CA⊥y轴,交抛物线于点A,点B在抛物线上,且在第一象限内,BE⊥y轴,交y轴于点E,交AO的延长线于点D,BE=2AC.
(1)用含m的代数式表示BE的长.
(2)当m=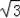 时,判断点D是否落在抛物线上,并说明理由.
时,判断点D是否落在抛物线上,并说明理由.
(3)若AG∥y轴,交OB于点F,交BD于点G.
①若△DOE与△BGF的面积相等,求m的值.
②连结AE,交OB于点M,若△AMF与△BGF的面积相等,则m的值是 .

解(1):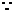 y=x2﹣mx﹣3,当
y=x2﹣mx﹣3,当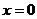 时,
时,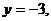
 C(0,﹣3),
C(0,﹣3),
∵AC⊥OC,
∴点A纵坐标为﹣3,
当y=﹣3时,﹣3=x2﹣mx﹣3,解得x1=m,x2=0(不合题意,舍去),
∴点A坐标(m,﹣3),
∴AC=m,
∴BE=2AC=2m.
(2)∵m=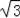 ,
,
∴点A坐标(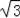 ,﹣3),
,﹣3),
∴直线OA为y=﹣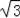 x,
x,
∴抛物线解析式为y=x2﹣ x﹣3,
x﹣3,
∴点B坐标(2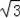 ,3),
,3),
∴点D纵坐标为3,
对于函数y=﹣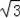 x,当y=3时,x=﹣
x,当y=3时,x=﹣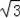 ,
,
∴点D坐标(﹣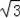 ,3).
,3).
∵对于函数y=x2﹣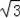 x﹣3,x=﹣
x﹣3,x=﹣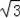 时,y=3,
时,y=3,
∴点D在落在抛物线上.
(3)
①∵∠ACE=∠CEG=∠EGA=90°,
∴四边形ECAG是矩形,
∴EG=AC=BG,
∵FG∥OE,EG=BG,
∴OF=FB,
∴EO=2FG,
∴BG=2DE,
∵DE∥AC,
∴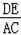 =
=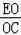 =
=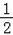 ,
,
∵点B坐标(2m,2m2﹣3),
∴OC=2OE,
∴3=2(2m2﹣3),
∵m>0,
∴m=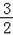 .
.
②∵A(m,﹣3),B(2m,2m2﹣3),E(0,2m2﹣3),
∴直线AE解析式为y=﹣2mx+2m2﹣3,直线OB解析式为y=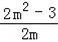 x,
x,
由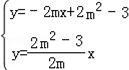 消去y得到﹣2mx+2m2﹣3=
消去y得到﹣2mx+2m2﹣3=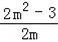 x,解得x=
x,解得x=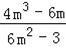 ,
,
∴点M横坐标为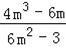 ,
,
∵△AMF的面积=△BFG的面积,
∴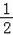 •(
•(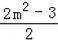 +3)•(m﹣
+3)•(m﹣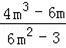 )=
)=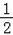 •m•
•m•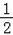 (2m2﹣3),
(2m2﹣3),
整理得到:2m4﹣9m2=0,
∵m>0,
∴m=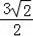 .
.
正确解答该题的关键在于,利用数形结合转化已知条件.
 浙公网安备33052302000911号
浙公网安备33052302000911号