由6根钢管首尾顺次铰接而成六边形钢架ABCDEF,相邻两钢管可以转动.已知各钢管的长度为AB=DE=1米,BC=CD=EF=FA=2米.(铰接点长度忽略不计)
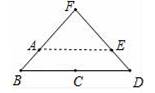
(1)转动钢管得到三角形钢架,如图1,则点A,E之间的距离是 米.
(2)转动钢管得到如图2所示的六边形钢架,有∠A=∠B=∠C=∠D=120°,现用三根钢条连接顶点使该钢架不能活动,则所用三根钢条总长度的最小值是 米.

图1 图2
解:(1)如图,
∵FB=DF,FA=FE,
∴∠FAE=∠FEA,∠B=∠D,
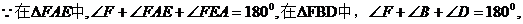
∴∠FAE=∠B,
∴AE∥BD,
∴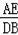 =
=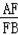 ,
,
∴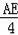 =
=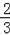 ,
,
∴AE= ,
,
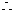 点A,E之间的距离是
点A,E之间的距离是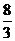 米.
米.
(2)如下图,作BN⊥FA于N,延长AB、DC交于点M,连接BD、AD、BF、CF.
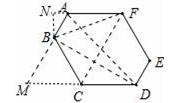
在RT△BFN中,∵∠BNF=90°,BN=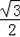 ,FN=AN+AF=
,FN=AN+AF= +2=
+2= ,
,
∴BF=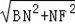 =
=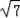 ,同理得到AC=DF=
,同理得到AC=DF=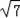 ,
,
∵∠ABC=∠BCD=120°,
∴∠MBC=∠MCB=60°,
∴∠M=60°,
∴CM=BC=BM,
∵∠M+∠MAF=180°,
∴AF∥DM,∵AF=CM,
∴四边形AMCF是平行四边形,
∴CF=AM=3,
∵∠BCD=∠CBD+∠CDB=60°,∠CBD=∠CDB,
∴∠CBD=∠CDB=30°,∵∠M=60°,
∴∠MBD=90°,
∴BD=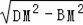 =2
=2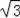 ,同理BE=2
,同理BE=2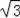 ,
,
∵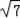 <3<2
<3<2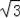 ,
,
∴用三根钢条连接顶点使该钢架不能活动,
∴连接AC、BF、DF即可,
∴所用三根钢条总长度的最小值3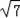 .
.
正确解答该题的关键在于,根据已知条件通过添加辅助线构造特殊三角形与相关的平行四边形.
 浙公网安备33052302000911号
浙公网安备33052302000911号