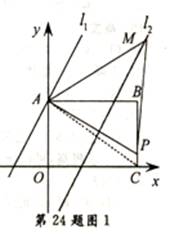
如图,在矩形ABCO中,点O为坐标原点,点B的坐标为(4,3),点A,C在坐标轴上,点P在BC边上,直线 :y=2x+3,直线
:y=2x+3,直线 :y =2 x-3
:y =2 x-3
(1)分别求直线 与x轴、直线
与x轴、直线 与AB的交点坐标.
与AB的交点坐标.
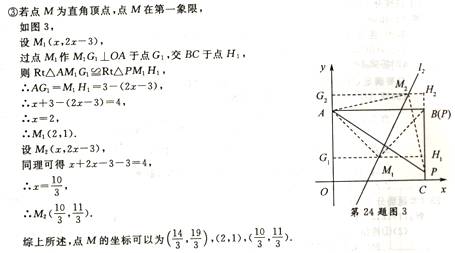
(2)已知点M在第一象限,且是直线 上的点,若∆APM是等腰直角三角形,求点M的坐标.
上的点,若∆APM是等腰直角三角形,求点M的坐标.
(3)我们把直线 和直线
和直线 上的点所组成的图形称为图形F.已知矩形ANPQ的顶点N在图形F上,Q是坐标平面内的点,且N点的横坐标 为x,请直接写出x的取值范围.
上的点所组成的图形称为图形F.已知矩形ANPQ的顶点N在图形F上,Q是坐标平面内的点,且N点的横坐标 为x,请直接写出x的取值范围.

答案



(3)①当N在直线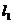 上时,x
上时,x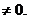
若N在点A的右侧,则作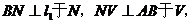 直线
直线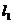 交
交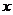 轴于
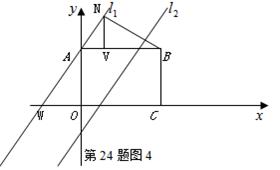
轴于 如图4
如图4
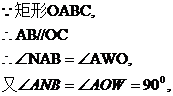
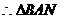 ∽
∽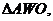
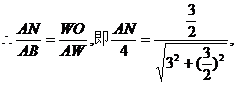
解得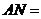
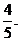
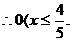
若N在点A的右侧,则作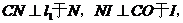 直线
直线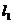 交
交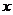 轴于
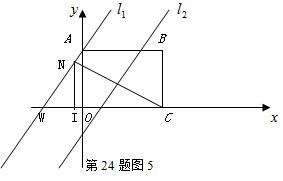
轴于 如图5
如图5
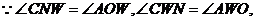
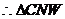 ∽
∽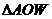
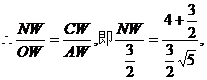
解得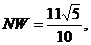
同理可得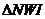 ∽
∽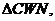
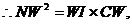
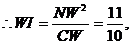
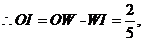
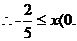
②当N在直线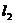 上时,
上时,
若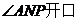 向右上方,点P在点C处,如图6,则作
向右上方,点P在点C处,如图6,则作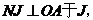 直线
直线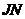 与线段
与线段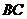 的延长线交于点K,
的延长线交于点K,
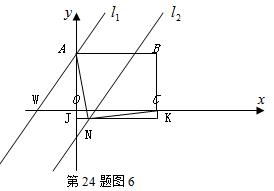
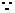 矩形ANPQ,
矩形ANPQ,
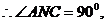
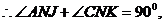
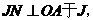 直线
直线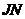 与线段
与线段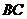 的延长线交于点K,
的延长线交于点K,
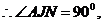
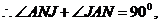
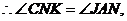
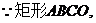
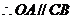
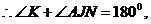
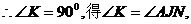
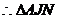 ∽
∽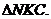
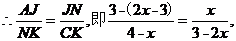
解得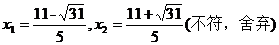
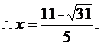
若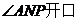 向右上方,点P在点B处,如图7,则作
向右上方,点P在点B处,如图7,则作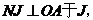 直线
直线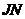 与线段
与线段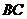 的交于点K,
的交于点K,
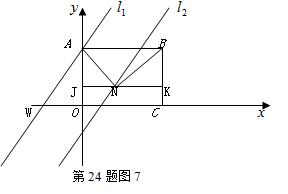
与上述情况雷同,同理可得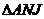 ∽
∽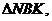
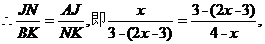
解得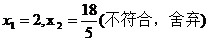
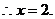
 若
若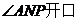 向右上方,则
向右上方,则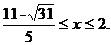
同理可得,若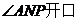 向左下方,则
向左下方,则![]()
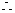 x的取值范围为:
x的取值范围为: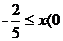 或
或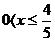 或
或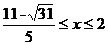 或
或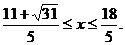
解析
正确解答该题的关键在于,领会题意,数形结合,分类讨论.
 浙公网安备33052302000911号
浙公网安备33052302000911号