解（1）：由折叠性质得：△ANM≌△ADM，
∴∠MAN=∠DAM，
∵AN平分∠MAB，∠MAN=∠NAB，
∴∠DAM=∠MAN=∠NAB，
∵四边形ABCD是矩形，
∴∠DAB=90°，
∴∠DAM=30°，
∴DM=AD•tan∠DAM=3×tan30°=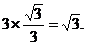

（2）延长MN交AB延长线于点Q，如图1所示：

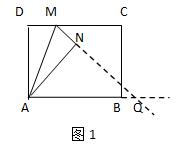
∵四边形ABCD是矩形，
∴AB∥DC，
∴∠DMA=∠MAQ，
由折叠性质得：△ANM≌△ADM，
∴∠DMA=∠AMQ，AN=AD=3，MN=MD=1，
∴∠MAQ=∠AMQ，
∴MQ=AQ，
设NQ=x，则AQ=MQ=1+x，
∵∠ANM=90°，
∴∠ANQ=90°，
在Rt△ANQ中，由勾股定理得：AQ²=AN²+NQ²，
∴（x+1）²=3²+x²，
解得：x=4，
∴NQ=4，AQ=5，
∵AB=4，AQ=5，
∴

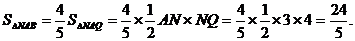
（3）过点A作AH⊥BF于点H，如图2所示：

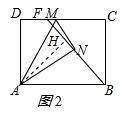
∵四边形ABCD是矩形，
∴AB∥DC，
∴∠HBA=∠BFC，
∵∠AHB=∠BCF=90°，
∴△ABH∽△BFC，
∴，
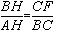∵AH≤AN=3，AB=4，
∴当点N、H重合（即AH=AN）时，AH最大，BH最小，CF最小，DF最大，此时点M、F重合，B、N、M三点共线，如图3所示：

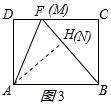
由折叠性质得：AD=AH，
∵AD=BC，
∴AH=BC，
在△ABH和△BFC中，

，
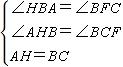∴△ABH≌△BFC（AAS），
∴CF=BH，
由勾股定理得：，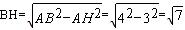
∴DF的最大值=DC-CF=．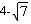

解答该题的关键在于，画出图形，数形结合，正确利用图中图形之间的特殊关系.