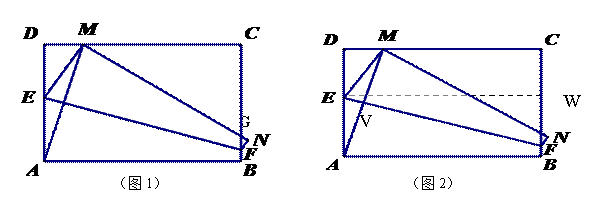
若在矩形ABCD中，AB=6，AD=4，将矩形进行折叠，使顶点A与CD边上的点M重合，折痕交AD于E，交BC于F，边AB折叠后BC与交于点G.
⑴若DM=1时，求DE和CG的长；
(2)设DM的长为x，梯形CDEF的面积为S，那么是否存在S的最大值？若存在，请求出这个最大值及此时x的值；若不存在，请说明理由.
答案
解(1)：如图1，由折叠得EM=AE,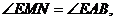
,
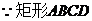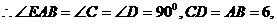
设DE=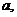
则
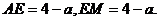
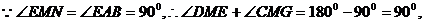
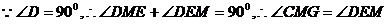
又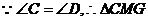
∽
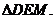
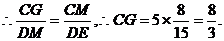
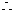
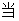
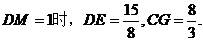
（2）当DM的长为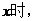
与解（1）同理可得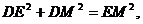
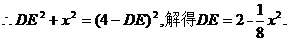
如图（2），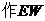
//
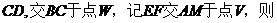
由折叠得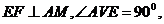
//
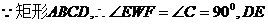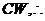四边形
//
∽
,
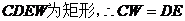
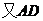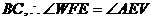
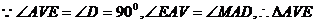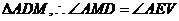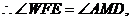又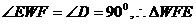
∽
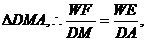
解得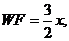
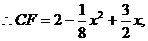
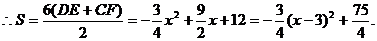
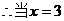时，S取到最大值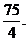
解析
求折叠问题中的线段长度、梯形面积等问题时，经常要用到勾股定理、相似三角形、三角函数等基础知识，要会灵活运用数形结合、方程求解、转化等思想方法。
浙公网安备33052302000911号