您当前的位置：首页 - 题库 - 解析

（2015年金华）图1，图2为同一长方体房间的示意图，图2为该长方体的表面展开图.

（1）蜘蛛在顶点处

     ①苍蝇在顶点B处时，试在图1中画出蜘蛛为捉住苍蝇，沿墙面爬行的最近路线；

     ②苍蝇在顶点C处时，图2中画出了蜘蛛捉住苍蝇的两条路线，往天花板ABCD爬行的最近路线和往墙面爬行的最近路线，试通过计算判断哪条路线更近？ 
（2）在图3中，半径为10dm的⊙M与相切，圆心M到边的距离为15dm，蜘蛛P在线段AB上，苍蝇Q在⊙M的圆周上，线段PQ为蜘蛛爬行路线。若PQ与⊙M相切，试求PQ的长度的范围.

答案

解：（1）①如答图1，连结 ，线段 就是所求作的最近路线.

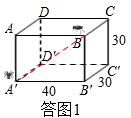
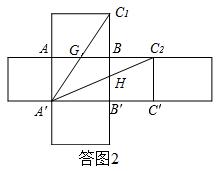
 ②两种爬行路线如答图2所示， 
由题意可得： 
在Rt△A'C'C2中， A'HC2=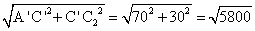  (dm)； 
在Rt△A'B'C1中， A'GC1=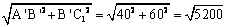 (dm)
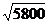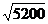∵＞，∴路线A'GC1更近.
  


（2）如答图，连接MQ， 
∵PQ为⊙M的切线，点Q为切点， 
∴MQ⊥PQ.
∴在Rt△PQM中，有PQ2=PM 2－QM 2= PM 2－100， 
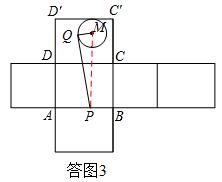
当MP⊥AB时,MP最短，PQ取得最小值，如答图3,
此时MP=30+20=50， 
∴PQ=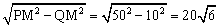  (dm).
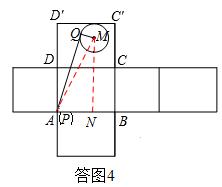
当点P与点A重合时, MP最长，PQ取得最大值，如答图4,
过点M作MN⊥AB，垂足为N， 
∵由题意可得 PN=25，MN=50， 
∴在Rt△PMN中， .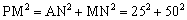
∴在Rt△PQM中，PQ=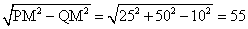  (dm).
综上所述， PQ长度的取值范围是 .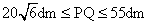


解析

【考查的主要知识点】长方体的表面展开图；双动点问题；线段、垂直线段最短的性质；直线与圆的位置关系；勾股定理.

【解题过程分析】（1）①根据两点之间线段最短的性质作答.
②根据勾股定理，计算两种爬行路线的长，比较即可得到结论.
（2）当MP⊥AB时,MP最短，PQ取得最小值；当点P与点A重合时, MP最长，PQ取得最大值.求出这两种情况时的PQ长即可得出结论.

【注意点】审题时注意示意图中包含的已知条件.

热门资源下载