A、B、C、D四种商品的单价分别为2元、3元、5元和7元.现从中选购了6件共花费了36元.如果至少选购了3种商品，则买了           件D种商品.

甲、乙两名运动员在圆形跑道上从A点同时出发，并按相反方向匀速跑步，甲的速度为每秒6米，乙的速度为每秒7米，当他们第一次在A点再度相遇时跑步就结束．则从他们开始出发（算第一次相遇）到结束（算最后一次相遇）共相遇次数是（　　）

A．13                                  B．14                                    C．42                                 D．43

小明学了计算机运算法则后, 编制了一个程序，当他任意输入一个有理数以后，计算机会计算出这个有理数的平方减去2的差．若他第一次输入- ,然后将所得结果再次输入，那么最后得到的结果是______．

某仓库在某天运进和运出一批货物，运进为“+”，运出为“-”，单位为“吨”．记录如下：+30，-15，+25，-10，-18，+40，-17，-23．

（1）若原库存为10吨，则当天最终库存多少吨？

（2）若运进运出每车费用50元，一车装5吨，则当天总运费为多少元？

邮政部门规定：信函重100克以内（包括100克）每20克贴邮票0.8元，不足20克重以20克计算；超过100克，先贴邮票4元，超过100克部分每100克加贴邮票2元，不足100克重以100克计算．
（1）若要寄一封重35克的信函，则需贴邮票多少元？
（2）若寄一封信函贴了6元邮票，问此信函可能有多少重？
（3）七（1）班有九位同学参加环保知识竞赛，若每份答卷重12克，每个信封重4克．请你设计方案，将这9份答卷分装在两个信封中寄出，使所贴邮票的总金额最少．

如图，数轴上标有2n+1个点，它们对应的整数分别是：

-n,-(n-1),-(n-2),……,-3,-2,-1,0,1,2……n-2,n-1,n,

为了确保从这些点中可以取出2015个，其中任何两个点之间的距离都不等于4，则n的最小值是          .

13个小朋友围成一圈做游戏，规则是从某一个小朋友开始按顺时针方向数数，数到第13，该小朋友离开；这样继续下去，直到最后剩下一个小朋友．小明是1号，要使最后剩下的是小明自己，他应该建议从（　　）小朋友开始数起．

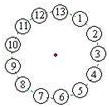
(A) 7号

（B）8号

（C）13号

（D）2号

狄摩根是19世纪英国数学家，在逻辑研究方面有突出贡献.在他中年时，有人问他：“您多大年龄了？” 狄摩根幽默地说：“我在公元年时是x岁.” 狄摩根出生在        年.

解方程

若k为整数，则使得方程(k-1999)x=2001-2000x的解也是整数的k值有（    ）.

(A) 4个     (B) 8个     (C) 12个     (D) 16个