如图，数轴上标有2n+1个点，它们对应的整数分别是：-n,-(n-1),-(n-2),……,-3,-2,-1,0,1,2……n-2,n-1,n,为了确保从这些点初中数学导学网|浙江安吉导学网络科技有限公司

您当前的位置：首页 - 题库 - 解析

如图，数轴上标有2n+1个点，它们对应的整数分别是：

-n,-(n-1),-(n-2),……,-3,-2,-1,0,1,2……n-2,n-1,n,

为了确保从这些点中可以取出2015个，其中任何两个点之间的距离都不等于4，则n的最小值是 .

答案

解：由题设，应连续取4个点，再空4个点，又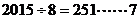，4+7=11

先在-5，-4，-3，-2，-1，0，1，2，3，4，5中取7个点，再从-n开始向右取4个连续的点，接着空4个点，再取4个连续的点，空4个点一共重复251次；类似的，从n开始向左取4个连续的点，接着空4个点，再取4个连续的点，空4个点一共重复251次，即可.

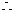2n+1=502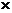8+11,解得n=2013,

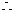n的最小值是2013.

解析

解答该题的关键在于，正确确定这2015个点的取法.