-
-
如图,
 中,
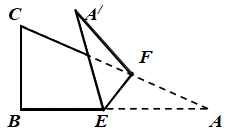
中, E,F分别是边AB,AC上的点,连结EF,将
E,F分别是边AB,AC上的点,连结EF,将 沿着EF折叠,得到
沿着EF折叠,得到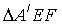 ,当
,当 的三边与
的三边与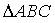 的三边有一组边平行时,
的三边有一组边平行时,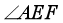 的度数不可能是 ( )
的度数不可能是 ( )A. 1200 B. 1050 C. 750 D. 450
-
-
-
甲、乙两名运动员在圆形跑道上从A点同时出发,并按相反方向匀速跑步,甲的速度为每秒6米,乙的速度为每秒7米,当他们第一次在A点再度相遇时跑步就结束.则从他们开始出发(算第一次相遇)到结束(算最后一次相遇)共相遇次数是( )
A.13 B.14 C.42 D.43
-
-
-
足球射门,不考虑其他因素,仅考虑射点到球门AB的张角大小时,张角越大,射门越好.如图的正方形网格中,点A,B,C,D,E均在格点上,球员带球沿CD方向进攻,最好的射点在( )

A.点C B.点D或点E
C.线段DE(异于端点) 上一点 D.线段CD(异于端点) 上一点
-
-
-
如图,平面直角坐标系中,平行四边形
 的顶点
的顶点 ,边
,边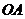 落在
落在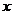 正半轴上,
正半轴上, 为线段
为线段 上一点,过点
上一点,过点 分别作
分别作 //
//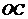 ,
, //
//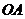 交平行四边形各边如图,若反比例函数
交平行四边形各边如图,若反比例函数 的图象经过点
的图象经过点 ,四边形
,四边形 的面积为6,则
的面积为6,则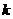 的值为( )
的值为( )A.18 B. 16 C. 12 D. 10

-
-
-
在发生某公共卫生事件期间,有专业机构认为该事件在一段时间没有发生大规模群体感染的标志为“连续10天,每天新增疑似病例不超过7人”。根据过去10天甲、乙、丙、丁四地新增疑似病例数据,一定符合该标志的是( )
A. 甲地:10天新增人数平均值为3,中位数为4
B. 乙地:10天新增人数平均值为1,方差大于0
C. 丙地:中位数为2,众数为3
D.丁地:10天新增人数平均值为2,方差为3
-
-
-
黑板上写有1,
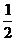 ,
,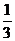 ,
,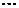 ,
,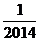 共2014个数字.每次操作先从黑板上的数中选取2个数
共2014个数字.每次操作先从黑板上的数中选取2个数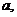
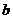 ,然后删去
,然后删去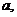
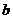 ,并在黑板上写上数
,并在黑板上写上数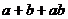 ,则经过2013次操作后,黑板上剩下的数是( )
,则经过2013次操作后,黑板上剩下的数是( )A. 2012 B. 2013 C. 2014 D. 2015
-
-
-
游泳者在河中逆流而上,于桥A下面将水壶遗失被水冲走,他继续向前游20分钟后,才发现水壶遗失,于是立即返回追寻水壶,在桥A下游距桥A2千米处追到了水壶,那么该河水的水流速度是( )
A. 1千米/小时 B.2千米/小时 C. 3千米/小时 D. 4千米/小时
-
-
-
已知点
 与点
与点 是一个平行四边形的四个顶点,则
是一个平行四边形的四个顶点,则 长的最小值为( )
长的最小值为( ) A. 4 B.
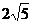 C.
C.  D.
D. 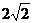
-
-
-
使得
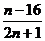 的值是整数的所有正整数
的值是整数的所有正整数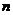 的个数有( )
的个数有( )A. 1个 B. 2个 C. 3个 D. 4个
-
-
-
13个小朋友围成一圈做游戏,规则是从某一个小朋友开始按顺时针方向数数,数到第13,该小朋友离开;这样继续下去,直到最后剩下一个小朋友.小明是1号,要使最后剩下的是小明自己,他应该建议从( )小朋友开始数起.
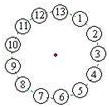
(A) 7号
(B)8号
(C)13号
(D)2号
-
浙江安吉导学网络科技有限公司 版权所有 浙ICP备2021004467号-1 浙公网安备33052302000911号
浙公网安备33052302000911号
※有关作品版权事宜请联系:13083908525 邮箱:zcb7525@163.com