解答
解(1):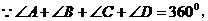
又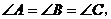
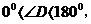

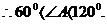
(2)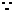 平行四边形DEBF,
平行四边形DEBF,
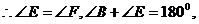
又由折叠得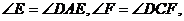
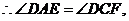
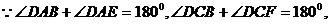
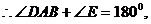
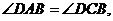
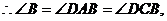
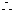 四边形ABCD是三等角四边形.
四边形ABCD是三等角四边形.
(3)当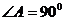 时,三等角四边形ABCD是正方形,则
时,三等角四边形ABCD是正方形,则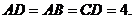
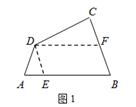
当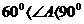 时,如图1,过点
时,如图1,过点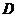 作
作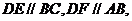 分别交
分别交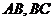 于点
于点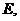 点
点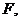 则
则
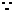
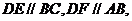
 四边形
四边形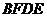 是平行四边形,
是平行四边形,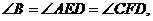
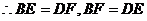
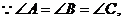
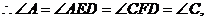
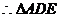 ∽
∽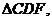
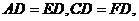
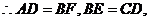
设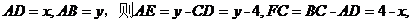
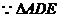 ∽
∽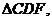
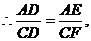
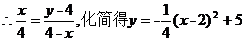
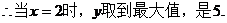 即当AD=2时,AB的长最大,其最大值是5.
即当AD=2时,AB的长最大,其最大值是5.
当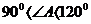 时,
时,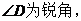 如图2,过点
如图2,过点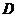 作
作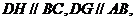 分别交
分别交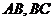 延长线于点
延长线于点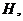 点
点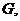 则
则
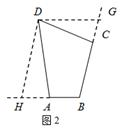
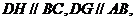
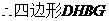 是平行四边形,
是平行四边形,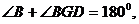
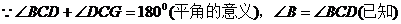
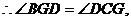
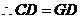
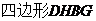 是平行四边形
是平行四边形
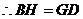
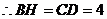
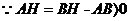
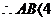
综上所述,当AD=2时,AB的长最大,其最大值是5.
此时,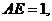 如图标3,作
如图标3,作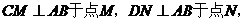 则
则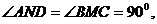
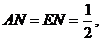
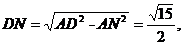
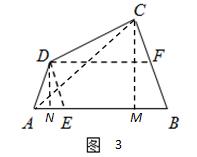
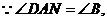
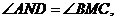
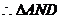 ∽
∽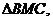
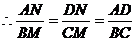
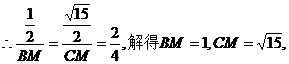
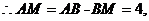
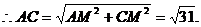
 当AD=2时,AB的长最大,是5,此时对角线AC的长=
当AD=2时,AB的长最大,是5,此时对角线AC的长=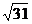 .
.
解析:正确解答该题的关键在于,依据题意,分情况画出图形,数形结合.
 浙公网安备33052302000911号
浙公网安备33052302000911号